どうも、のなめです。
現在、機械設計技術者試験を受検するために機械力学について勉強しています。その中で今回は機械力学の基礎的な部分、『静力学』についてまとめてみます。力学の中でかなり基本的な部分になるので、覚えて損はないと思います!
『静力学』とは?
物体に複数の力が働いているとき、それぞれの力の総和やモーメントの総和はともに『ゼロ』になった場合(釣り合っているとき)、物体は静止状態になります。そのときに力のつり合いについて論じる分野ということです。
たとえば簡単なところで、床に置かれたリンゴは、床が傾いていたり、横から人が押したりとかしていなければ、その場にとどまり続けます。これは「リンゴに加えられている重力の大きさと、床からの垂直抗力の大きさが同じ(釣り合っている)」のため、止まっています。
もし、重力のほうが大きいとなれば、床にめり込んだり!?と考えられますね!
『静力学』の対義語として『動力学』があります。動力学については後日投稿予定です。

力のつり合いと合成・分解
物体を動かす場合には力が必要ですが、もし静止している状態であれば前述の通り、力が釣り合っているといえます。
また、下図のように力の大きさと方向を矢印で表すことができ、「ベクトル量」と呼びます。下の左図と右図は作用線上で作用点を移動させた状態ですが、どちらも物体に与える力、向きは同じものになります。(物体にほかに力が加わっていなければ、右斜め上の方向に動き出しそう!?)
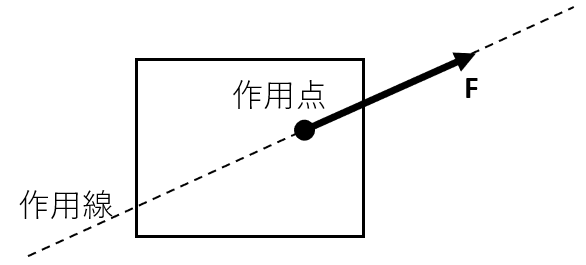
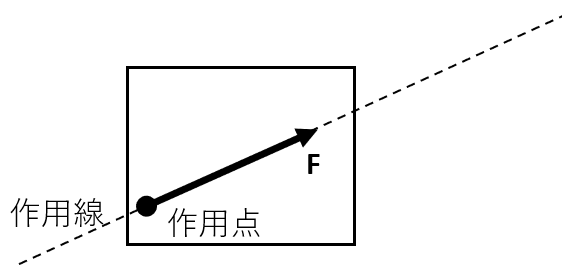
ベクトル量(力と方向)が分かったら、作用線をイメージしよう!!!
作用点を移動させることで、計算時に考えやすくなったりします。
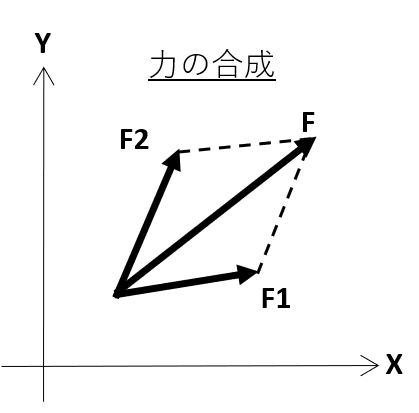
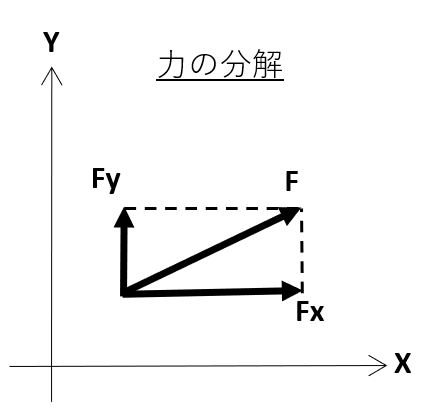
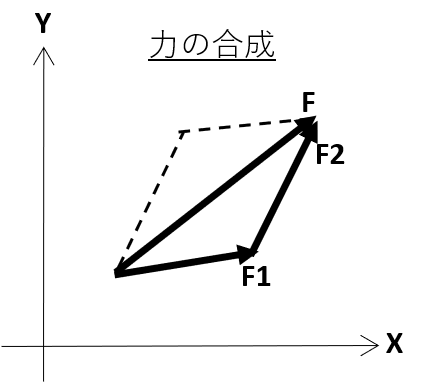
『力の合成・分解』は下図のようになります。
力の合成については、F = F1 + F2となり形状的には平行四辺形みたいな感じになっていますね!合成をすることで、2つの力が加わることで、合力(合わさった力)がどの方向に力が働いているかが分かります。また下図ではF1,F2と二つの力の合成ですが、3つ以上の場合は、F1+F2=F12 → F12+F3=F123のように順を追って合成することができます。
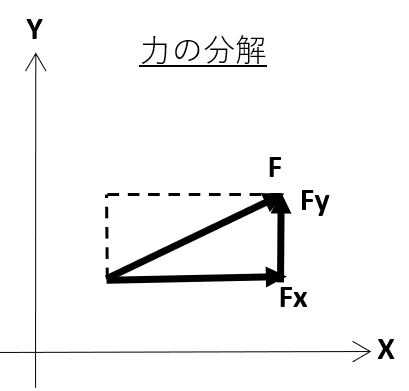
力の分解については、Fx + Fy = Fとなり形状的には長方形みたいになります。分解は力のつり合いについて計算するときに必要になります。下図では水平(Fx)垂直(Fy)となっていますが、力は斜めに働いているので、sinΘやcosΘ等、三角関数の知識も必要になるので要注意!
力の合成、分解は上図以外にも下図のような感じにも分解できるので覚えておくとよいでしょう!
力のモーメント
『力のモーメント』とは、物体の任意の点まわり(軸まわり)に働く、物体を回転させる能力になります。「力F」と「任意の点から、その力が作用している点(距離:r)」との積(掛け算)をした大きさになり、単位は(N・m)となります。
『どういうこっちゃ!?』というかたに、まずは、力×距離ってことを覚えていただければ・・・
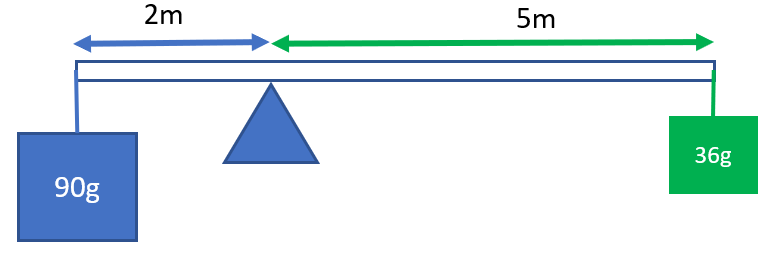
あとモーメントの例題としてよく出されるのは、てこの原理があります。てこの原理というと、『小さな力で大きなものを動かす』ですね。
下図を見ると、「左の青い物体(90g)と距離(2m)の積」と、「右の緑の物体(36g)と距離(5m)の積」がどちらも180(g・m)となっています。値が同じということは釣り合っている状態といえますね!(ここでは、重力加速度を無視しています。ごめんなさい。)
重力と重心
『重力』とは、物体が下向きに受ける力のことを言い、ものを置いたり、人が立ったりできるのは重力の働きがあるからです。また重力は万有引力とも呼ばれたりします。(ニュートンのりんごの木が有名ですね!!!)
重力では下記の式で求めることができます。「ニュートンの運動方程式」である運動の第2法則「F=ma」のほうが聞きなじみがあるかもしれないですね!この「a」は加速度なので、ここが重力加速度(g=9.8m/s^2)に置き換えることができます。
重力 = 質量 × 重力加速度 (F = mg)
『重心』とは簡単に言えば物体の中心になりますが、物体によっては中心位置にないものもあります。
物体の中心に重心があるものというとボールのような球体や、一様な丸棒、平板などシンプルな形状だと中心にあることが多いですね。
反対に物体の中心にないものとして、ごつごつした岩であったり、野球のバットなんかは中心とは離れていることが何となくわかりますよね!
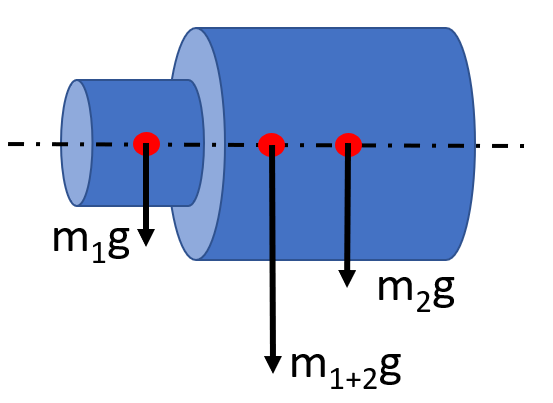
例として下図のような段付きの軸の重心を確認してみますが、径が細いほうの重心m1gと太いほうm2gとしたとき、それぞれの中心位置に間に全体の重心(m1+2g)が存在することになります。(計算で重心位置を求めることもできます。)
ポイントとして「径の細いほうと太いほう、それぞれの重心を求める」その合力の位置が「バランスが取れるところ」になります!
ちなみに、小学校くらいの掃除の時間にほうきの持つところを手に乗せてバランスをとって遊んだこともある人もいるかと思います。あれも重心の作用線が手に来るようにするとバランスよくまっすぐな状態を保つことができるのです。(しっかり掃除もしましょう!)
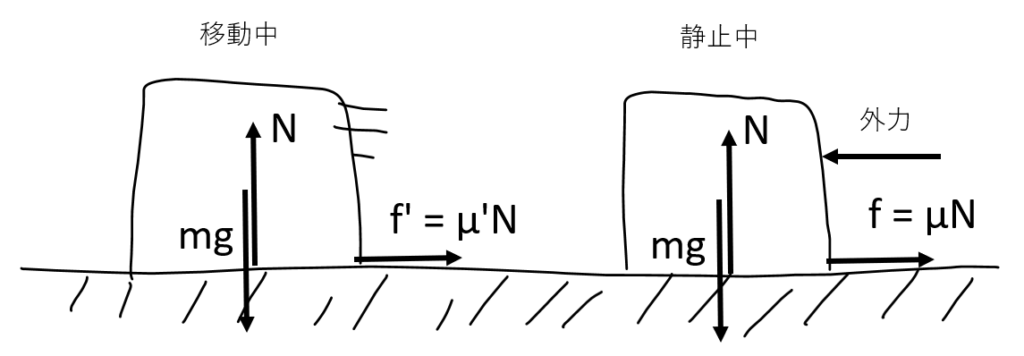
摩擦力
『摩擦力』はなめらかではない面で、外力を加えた方向(運動する方向)に対して、反対向きに作用する力です。また試験問題等で「なめらかな面(摩擦力を考慮しない)」「なめらかなではない面(摩擦力を考慮する)」となっていますので、問題文をよく読まないといけないですね。
摩擦力は、下記の式で表されます。垂直抗力(N)については、「1.『静力学』とは?」にもありますが、重力と同じなので、N = mgとなります。摩擦係数(μ)は、試験問題等では、問題文中に決められていたりしますが、一般的に物質によってある程度決まっているので必要な時に調べてみたください!
f = μN ( f = 摩擦力、μ = 摩擦係数、N = 垂直抗力)
摩擦力には、『静止摩擦力』と『動摩擦力』がありますので、ちょっとだけ紹介します。
静止摩擦力は、名前の通り物体が止まっているときの摩擦力になります。地面に設置している物体に徐々に力を加えていくと、いづれ動き出します。その動きだす瞬間までの摩擦力になります。この動き出す瞬間の摩擦力を、『最大静止摩擦力』と呼びます。
動き出したあとは、動摩擦力に変わっていきます。
静止摩擦力と動摩擦力、それぞれにかかる摩擦係数を『静止摩擦係数』『動摩擦係数』と呼び、一般的に動摩擦係数より、静止摩擦係数のほうが(静止摩擦係数 > 動摩擦係数)が大きくなっていますので覚えておいてください。
※下図の場合、μを静止摩擦係数、μ’を動摩擦係数としています。
まとめ
静力学についてまとめましたが、高校で学んだ物理の内容ですね。。。つり合いや、てこの原理にいたっては小学校の理科の授業で学んだりしてますよね。すごい基礎的な内容だと痛感しています。忘れかけてる部分や曖昧な部分が、少し振り替えたりできたかな!
ちなみに下記の本で勉強しています。「基礎勉強するのにいい本ないかな」といろいろ調べて本屋さんに行きましたが、自分は下記が合っていそうと思い選びました。どうやら学生向け?の教科書的な感じでよかったです。あと力学に入る前に数学について触れていたのはよかったかな!

あと、機械設計技術者試験に向けて下記を使用しています。機械力学だけでなく、材料力学や制御工学熱工学等、各分野についてのポイントが抑えられています。ただ1冊にまとまっているので、ある程度勉強してきた人向けな感じがしますね。。。

本記事で力学を学ぶきっかけになれば幸いです。


