どうも、”のなめ”です。
QC検定受験に向けて勉強していますが、そこで勉強した『相関分析』についてメモします。
とはいいつつ、勉強してもいきなり完全には理解できるはずもないので、試験のためにメモして自分が覚えやすい感じで書いてますので、ご了承ください。
『相関分析』とは?
相関分析とは、異なる2つのデータ(例えばXとY)に関係性があるか(関係性が強いか)を数値で分析する方法。
計算した数値は、「 -1 ≦ r ≦ 1 」の値になり、『 r 』を相関係数といいます。
相関係数の値が1(ー1)に近づくにつれて『高い正(負)の相関がある』となり、0になるにつれて『相関がない』となる。下記が散布図にプロットした時になります。各点(数値)を計算すると、相関の強さが分かるようになります。
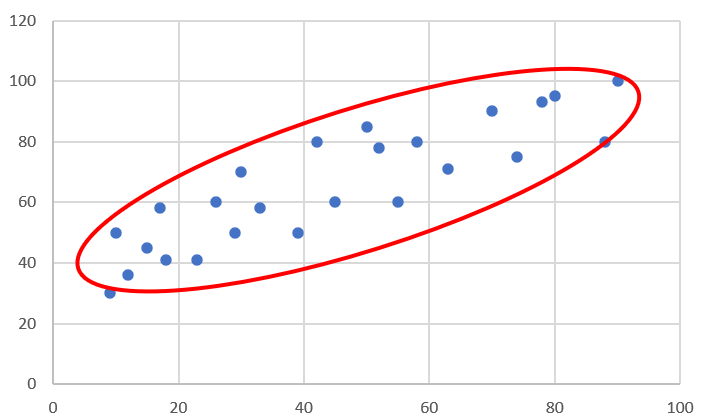
0.7 < r ≦ 1.0 【強い正(負)の相関がある】※下記はr = 0.87の場合
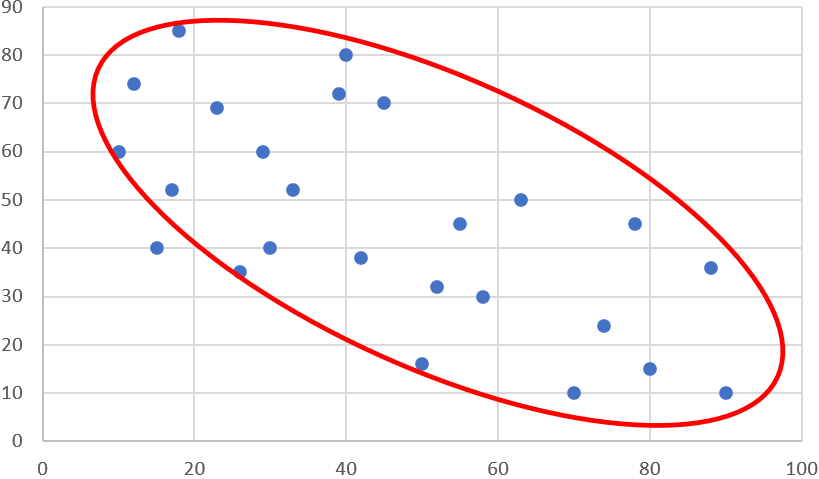
0.4 < r ≦ 0.7【比較的強い正(負)の相関がある】※下記はr = -0.6の場合(ここは負の相関を図示)
0.2 > r ≦ 0.4【弱い正(負)の相関がある】
※ここは割愛、0.4 < r ≦ 0.7ときより赤い楕円が円に近づきます。
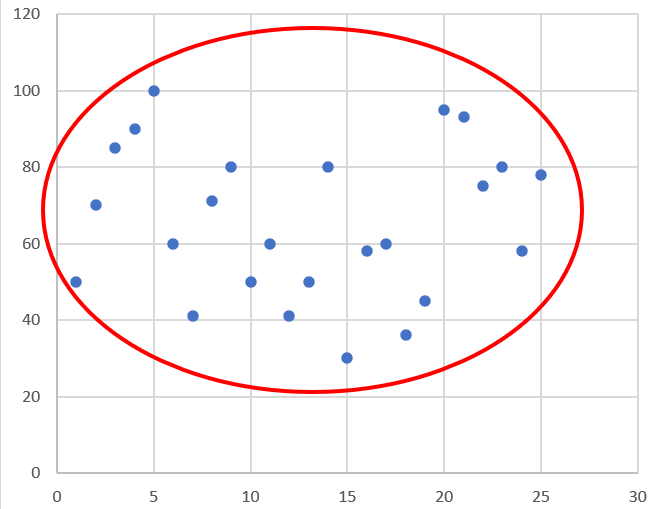
0.0 ≦ r ≦ 0.2【ほとんど相関はない】※下記はr = 0の場合
赤い楕円が直線に近づくにつれて相関係数の値が大きく(相関が高く)、円に近づくにつれて相関係数の値が小さく(相関がなく)なります。
また、楕円が右肩あがりだと正の相関、右肩下がりだと負の相関になります。
ざっくりこんな感じ!簡単ですね!
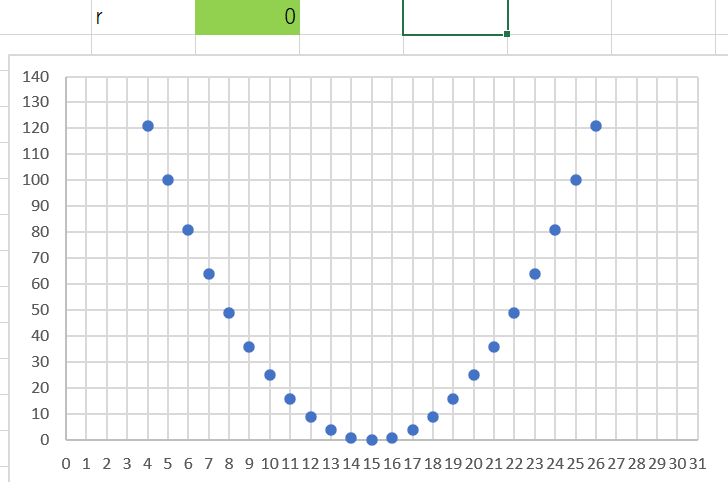
ちなみに、相関係数が「0」になる場合でも、すべてが「相関がない」とは言い切れないので注意が必要です。下記は、2次関数になるようにプロットして計算すると「0」になります。
『相関係数』を出す計算は?
相関係数を出すには、下記の計算をします。左下を文字式にしたのが右下になります。
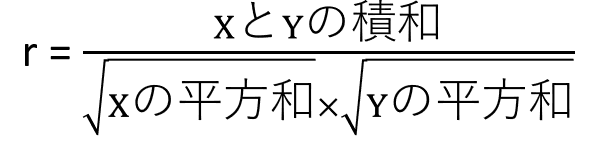
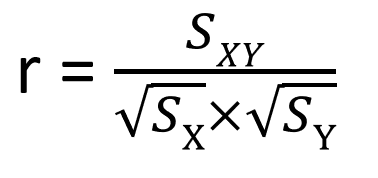
Xの平方和はこちら。「Xの各値を2乗した総和」から「Yの各値の総和の2乗/データ数」を引くことで算出されます。
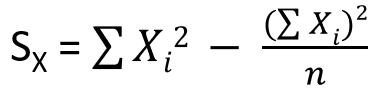
Yの平方和はこちら。Xと同様で「Yの各値を2乗した総和」から「Yの各値の総和の2乗/データ数」を引くことで算出されます。
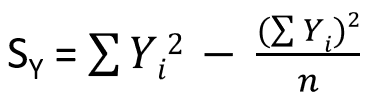
XとYの積和はこちら。X,Yの平方和と考え方は似てるかなと思います。「Xの各値とYの各値を掛けた総和」から「Xの総和とYの総和をかけた値/データ数」を引くことで算出されます。
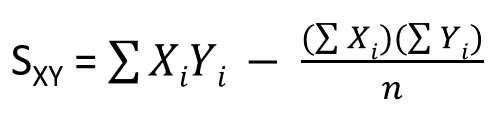
平方和については、相関分析以外でも使用するので、計算方法は覚えておいて損はないかなと思います。
寄与率って?(決定係数)
寄与率とは、相関係数を2乗した値になり、決定係数とも呼ばれるそう。
相関係数では「 -1 ≦ r ≦ 1 」の範囲を取りましたが、rを2乗するので、寄与率では「 0 < r^2 < 1」の範囲になります。
Xの値に対してYの値にどれだけ影響しているか(影響度合い)を示しているんですね。相関係数が「1」や「-1」に近づくほどr^2は「1」に近づくので影響度合いが強いということですね!
また、相関係数ではルート(√)が入って計算が少しだけ手間になりますが、r^2すると、ルートが消えるので、少しだけ計算が楽に感じるかな?
まとめ
相関分析について簡単にまとめてみました。正直、試験時にしか使わなそうな気もしていますが、知っていることで役に立つこともあると思いますので、お役に立てればと思います。